Last checked from ConnectWise official status page 3 min. 29 sec. ago
All-in-one MSP technology management software.
ConnectWise not working for you?
Report an outageThis chart represents ConnectWise service health over the last 24 hours, with data points collected every 15 minutes based on issue reports, page visits, and signal strength. Sign up for free to see more ConnectWise status data.
View and upvote the most commonly reported ConnectWise issues to help us better indicate the service status.
Have a different problem with ConnectWise?
Report an outage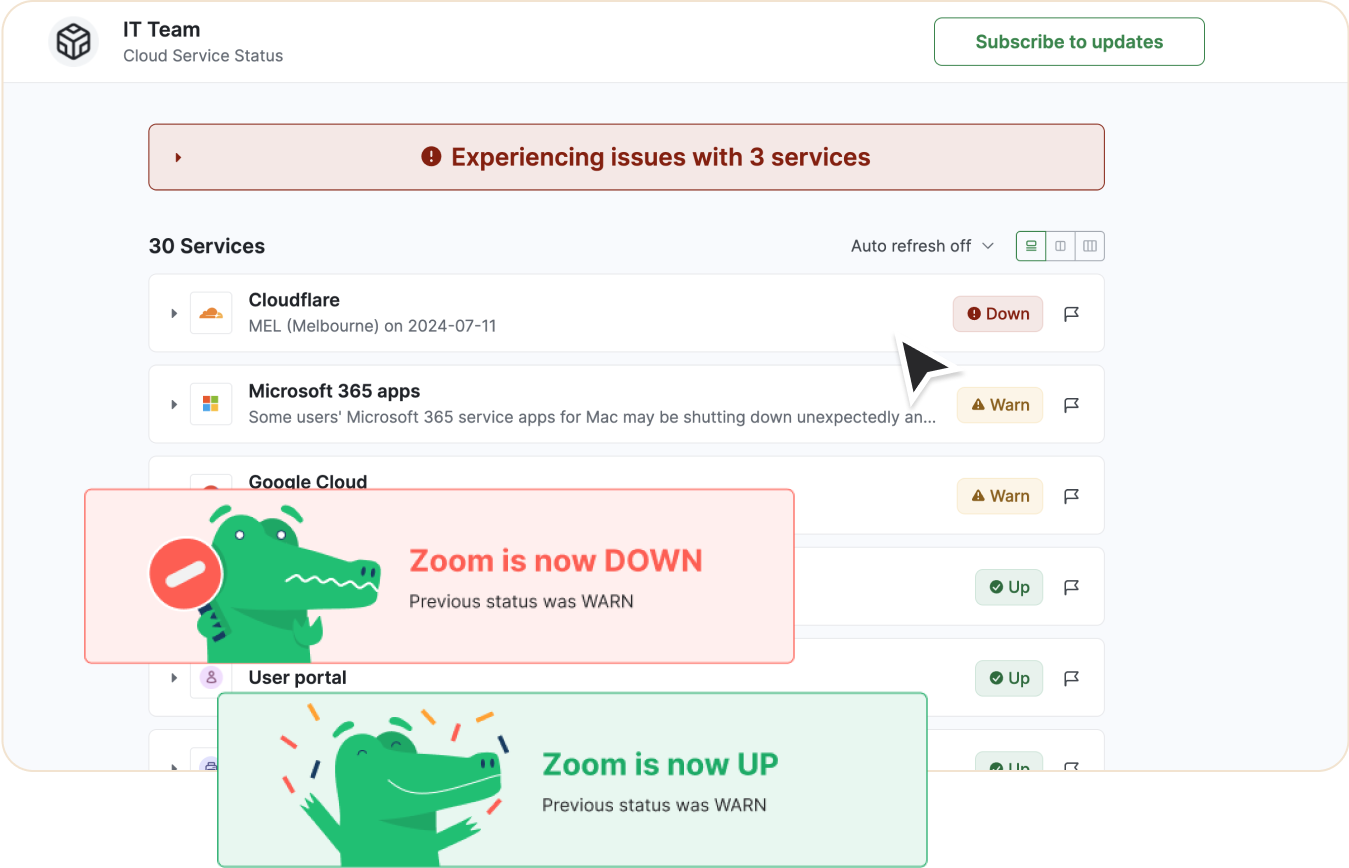
Follow the recent outages and downtime for ConnectWise in the table below. If you're experiencing a problem now, check the current ConnectWise status or report it.
| Incident Name | Duration | Started | Severity |
|---|---|---|---|
|
Co-managed Backup: Issues at US2 and US5 Acronis Data Center.
|
1d 2h 9m |
Warn
|
|
|
Co-managed Backup: Issues at US2 and US5 Acronis Data Center.
|
3h 35m |
Maint
|
|
|
Co-managed Backup: Issues at US2 and US5 Acronis Data Center.
|
55m |
Warn
|
|
|
QuickBooks OnPrem | ReceiveResponseXML Failed Error
|
5h 25m |
Warn
|
|
|
Investigating - RMM Network Monitoring syncing delay and failures
|
40m |
Warn
|
Stay updated with instant alerts for ConnectWise outages by signing up now!
You can also monitor any service or website on your status page
View details of the current ConnectWise status below. If the status shows "Up" but you're still experiencing issues, you can report a problem such as connectivity issues, outages, or slow performance. These issues are commonly reported when ConnectWise is down or facing partial disruptions.
Stay updated with instant alerts for ConnectWise outages by signing up now!
With features designed to cover all your needs for monitoring and communicating outages or downtime, StatusGator keeps your team connected and informed. Stay updated on ConnectWise outages, potential problems, and its current status in real-time, ensuring you're always prepared to act.
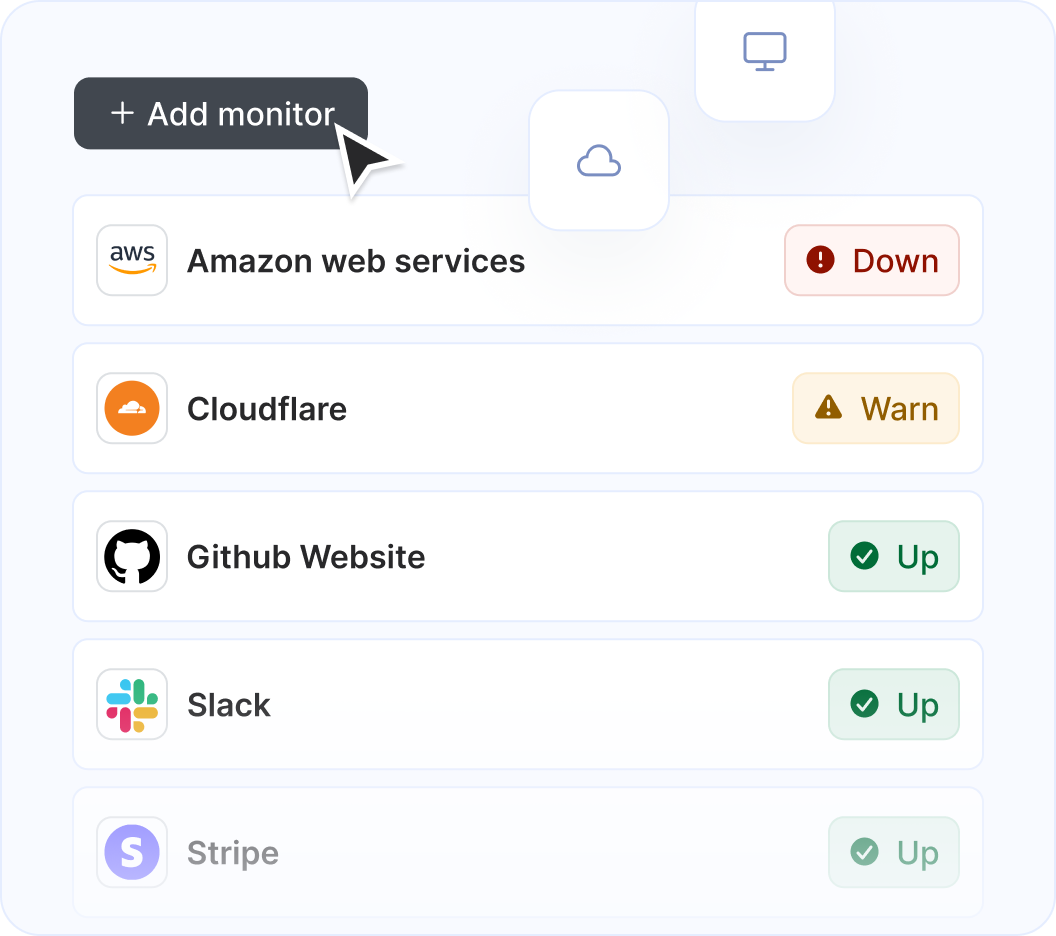

StatusGator monitors over 4,000 cloud services, hosted applications, and websites. Just add what you need to the list, and we'll automatically aggregate their statuses into a single page. You'll receive notifications for any issues affecting you and your page subscribers.
Start monitoring for free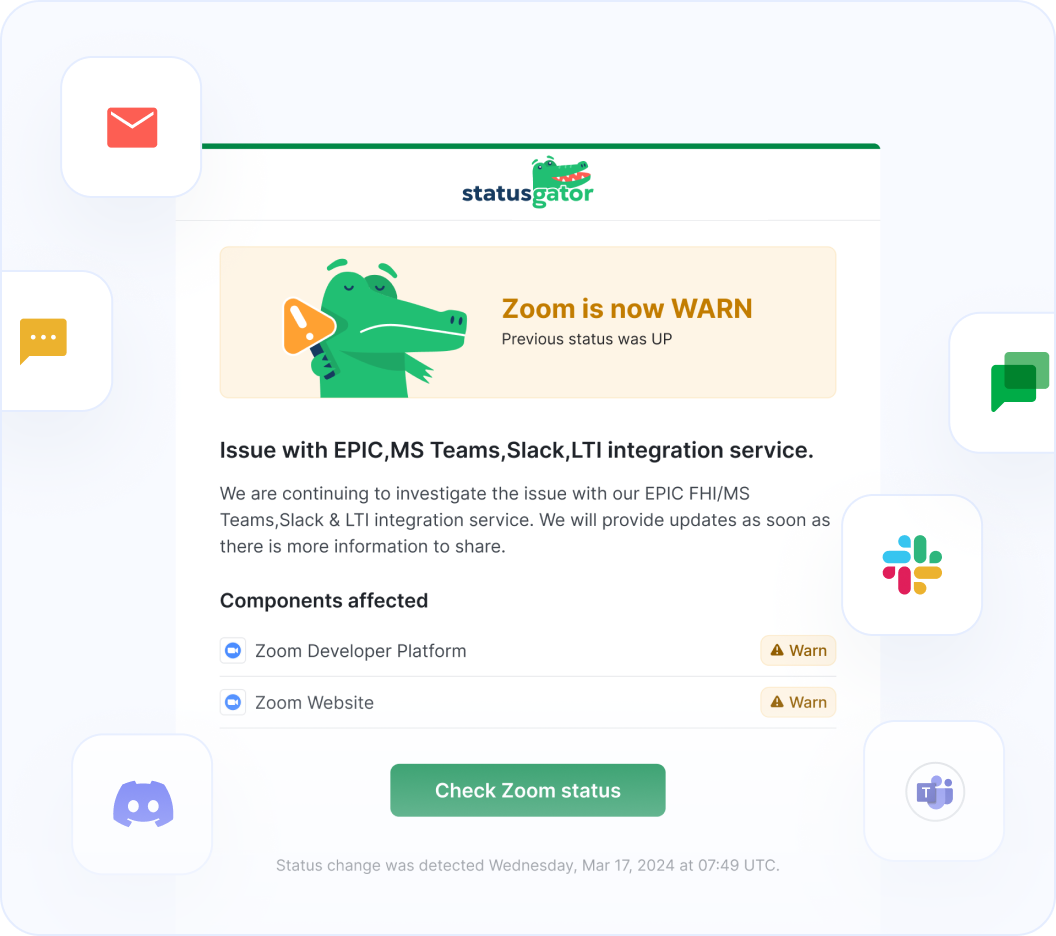
StatusGator monitors all of your services and websites and sends your team instant notifications when they go down. Stay abreast of issues that affect your team with notifications: in email, Slack, Teams, or wherever your team communicates.
Start monitoring for free
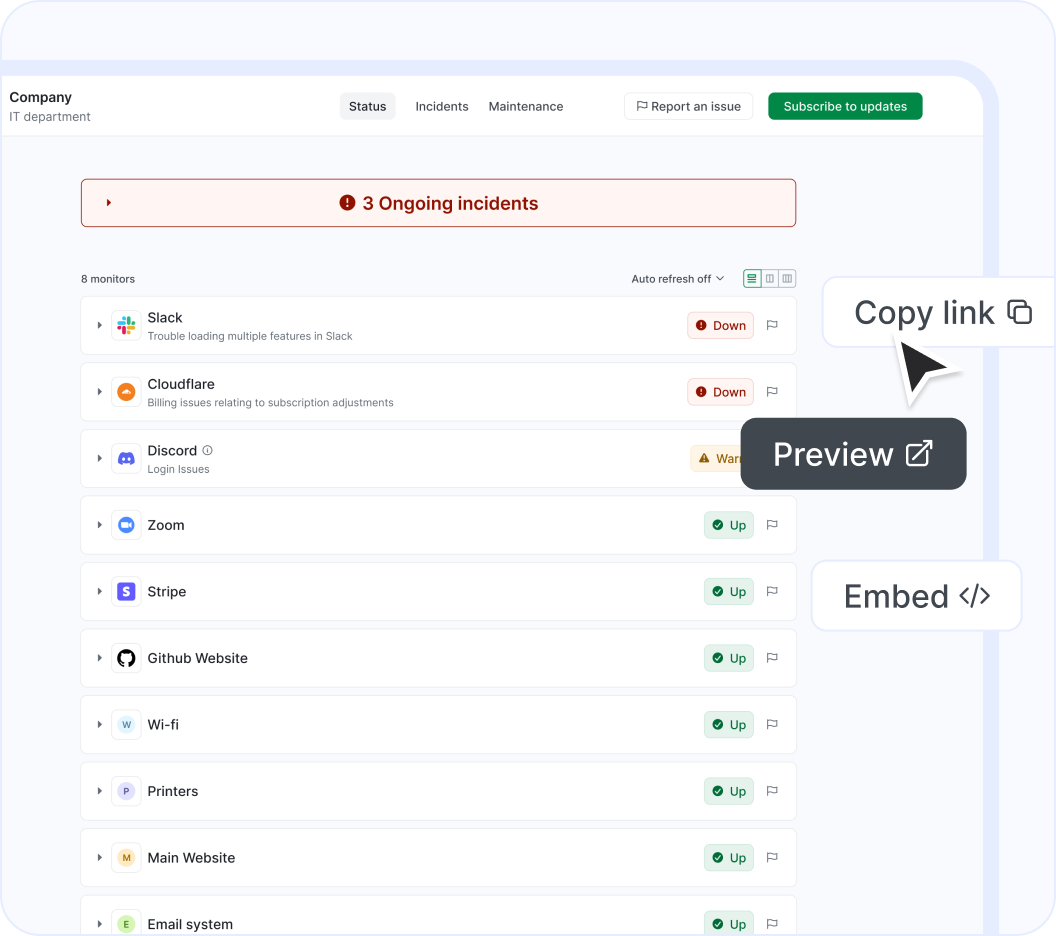

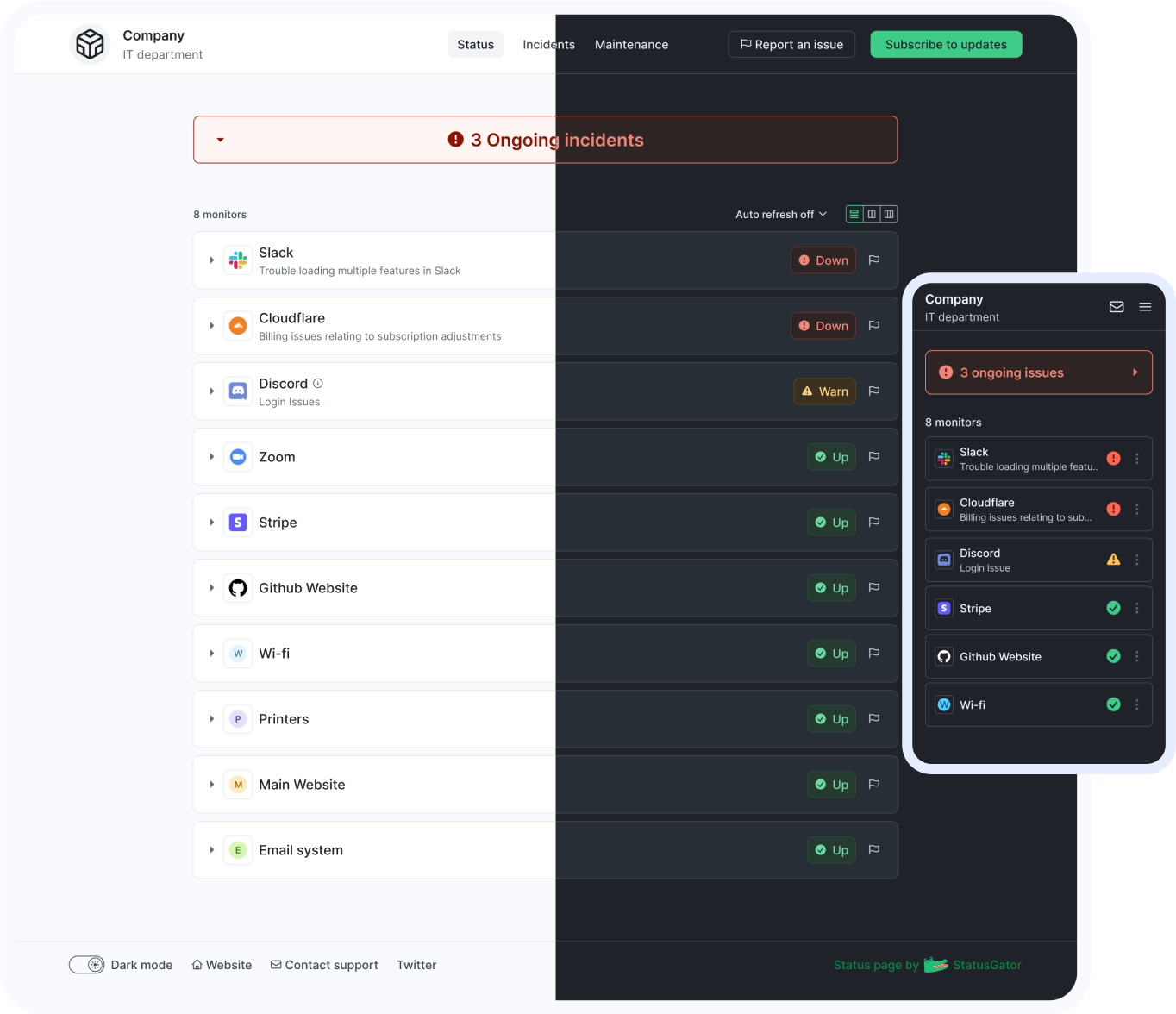
Easily notify your end-users of outages using a customizable status page. Display cloud services or websites, as well as any custom monitors you add manually. Create multiple status pages tailored to different needs, customize them, and embed them for maximum effectiveness.
Start monitoring for freeConnectWise (All-in-one MSP technology management software) is a an APIs, CRM, IT, and Project Management solution that StatusGator has been monitoring since June 2022. Over the past over 2 years, we have collected data on on more than 1,087 outages that affected ConnectWise users. When ConnectWise publishes downtime on their status page, they do so across 38 components using 4 different statuses: up, warn, down, and maintenance which we use to provide granular uptime metrics and notifications.
If you're wondering, "Is ConnectWise down?", or need to know its current status, we've got you covered. Our platform tracks every reported outage, performance issue, and maintenance window to ensure you're informed. Whether ConnectWise is experiencing a problem now or has recently resolved one, our detailed history keeps you updated.
More than 300 StatusGator users monitor ConnectWise to get notified when it's down, is under maintenance, or has an outage. This makes it one of the most popular CRM services monitored on our platform. We've sent more than 119,700 notifications to our users about ConnectWise incidents, providing transparency and peace of mind. You can get alerts by signing up for a free StatusGator account.
If we detect a potential ConnectWise outage or other issue before it was reported on the official status page we will send an Early Warning Signal notification to StatusGator subscribers. We can often detect issues before they are officially acknowledged by the provider, giving you a head start on resolving any potential problems.
If ConnectWise is having system outages or experiencing other critical issues, red down notifications appear on the status page. In most cases, it means that core functions are not working properly, or there is some other serious customer-impacting event underway.
Warn notifications are used when ConnectWise is undergoing a non-critical issue like minor service issues, performance degradation, non-core bugs, capacity issues, or problems affecting a small number of users.
ConnectWise posts separate notifications for planned maintenance work. StatusGator will notify subscribers when ConnectWise enters a pre-planned maintenance window, keeping you up to date.
When ConnectWise posts issues on their status page, we collect the main headline message and include that brief information or overview in notifications to StatusGator subscribers.
When ConnectWise has outages or other service-impacting events on their status page, we pull down the detailed informational updates and include them in notifications. These messages often include the current details about how the problem is being mitigated, or when the next update will occur.
Because ConnectWise has several components, each with their individual statuses, StatusGator can differentiate the status of each component in our notifications to you whenever a particular component is down. This means, you can filter your status page notifications based on the services, regions, or components you utilize. This is an essential feature for complex services with many components or services spread out across many regions.
Stay updated with instant alerts for ConnectWise outages by signing up now!
Can’t find your question? Email us to arrange a time to discuss. We’d love to chat!